ORDINAL DATA: INFERENCE

A. Procedure for data without ties:
1. Compute gamma.
2. Determine N.
3. Look up p-value in table (see appendix). Note: a directional hypothesis (positive or negative is specified) uses a one-tailed test; a nondirectional hypothesis or null hypothesis uses a two-tailed test.

Example: Data without ties

Corporation	# of favorable court decisions	Amount of political contributions
C	5	500,000
D	4	300,000
Q	3	400,000
R	2	100,000
V	1	200,000

Q: Can this association be generalized to the whole population when the hypothesis says: "There is a positive association between decisions and contributions"?
A: Note that this is a directional hypothesis since "positive" is specified.

Compute gamma: fa & fi

0		0
1		0
1		1
3		0
3		1
8 = fa	N = 5	2 = fi

Now look up the Significant Probability Value (scroll to the upper right corner for gamma).  It will look something like this: (G =.60)

		Two-tailed test		One-tailed test
N	p = .05		p = .01	p = .05	p = .01
5	1.000		-----	0.800	1.000
6

An N of 8 (0.571) is necessary, since the example's N is 5 (0.800> .60), it is not generalizeable.

B. Procedure for data with ties: Z =

Where: = |fa - fi |- {N / [2(R-l)(C-l)]}

fa & fi are computed same as for gamma

R = # of rows

C = # of columns

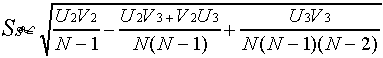
Assumptions: N > 10

Where: U₂ = sum of product of row totals taken two at a time.
V₂ = " " " " column totals taken two at a time.
U₃ = " " " " row " " three " " " .
V₃ = " " " " column " " " " " " .
*note if there is not a third row or column then U3 or V3 = 0

Example: Data with ties:

		Attractiveness
		Above Average	Medium	Below Average
Votes	Hi	22	23	6	51
received	Lo	14	31	14	59
		36	54	20	110

Q: Can this be generalized to the whole population of elected officials?

A: = "corrected S" (called S hat)

= "standard error of corrected S"

= | 1312 - 592 | - 110/[2(2-1)(3-1)] = 692.5

U₂ = 51(59) = 3009
V₂ = 36(54) + 36(20) + 54(20) = 3744
U₃ = 0
V₃ = 36(54)(20) = 38880

=

so Z = 692.5 / 305.94 = 2.26

Look up Z on p - value table in appendix. p < .05 so yes, it can be generalized.

*This is not a directional hypothesis so it is a two-tailed test

table of contents

homework

next lesson